Statystyczna kontrola procesu (SPC) to potężne narzędzie wykorzystywane przez przemysł do monitorowania i zarządzania procesami, zapewniają spójność i jakość produkcji.
Kluczem do zrozumienia SPC jest rozkład normalny, a dokładniej jego koncepcja, znana również jako rozkład Gaussa lub krzywa dzwonowa. Zrozumienie właściwości rozkładu normalnego jest niezbędne do skutecznego sterowania i optymalizacji procesu.
Co to jest rozkład normalny?
Rozkład normalny jest podstawowym pojęciem w statystyce i teorii prawdopodobieństwa. Charakteryzuje się symetryczną krzywą w kształcie dzwonu, w której większość punktów danych skupia się wokół wartości średniej, a mniejsza ilość punktów jest oddalonych od średniej w obu kierunkach. W idealnie normalnym rozkładzie średnia, mediana i moda są równe, a krzywa jest w pełni zdefiniowana przez jej średnią i odchylenie standardowe.

Rozkład normalny i jego znaczenie w SPC
Identyfikacja zmienności procesu
SPC ma na celu zidentyfikowanie i zminimalizowanie zmienności procesu. Gdy dane mają rozkład normalny, umożliwia to efektywne wykorzystanie technik statystycznych do zrozumienia zachowania procesu. Odchylenia od rozkładu normalnego mogą wskazywać na niestabilność procesu, skłaniając do dalszej analizy i działań korygujących.
Ustalenie granic kontrolnych
Wykresy kontrolne są podstawowym narzędziem w SPC, używanym do monitorowania zmian procesu w czasie. Zakładając rozkład normalny, granice karty kontrolnej można dokładnie obliczyć na podstawie średniej i odchylenia standardowego danych.
Granice kontrolne działają jak ograniczniki, wskazując dopuszczalny zakres zmienności dla stabilnego procesu. Punkty danych wykraczające poza granice sygnalizują zmienność spowodowaną szczególnymi przyczynami. Motywuje to do badania ewentualnych zmian lub problemów w procesie.
Dokładna analiza zdolności procesu
Analiza zdolności procesu ocenia, jak dobrze proces może wytwarzać produkty w określonych granicach. Zakładając rozkład normalny, można obliczyć wskaźniki zdolności, takie jak Cp, Cpk, Pp i Ppk, co zapewnia jasne zrozumienie zdolności procesu do spełnienia wymagań.
Informacje te są kluczowe dla działań na rzecz doskonalenia procesów i ustalania realistycznych celów produkcyjnych.
Skuteczna analiza przyczyny
Założenie normalności umożliwia stosowanie różnych testów i metod statystycznych, co ułatwia wskazanie źródła odchyleń i wdrożenie skutecznych rozwiązań.
Określenie wielkości próbki
W SPC wybór odpowiedniej wielkości próbki jest niezbędny do uzyskania wiarygodnych wyników. Kiedy dane mają rozkład normalny, określenie wielkości próby staje się prostsze, co prowadzi do dokładnych wniosków na temat całej populacji.
Jak p-value jest powiązany z rozkładem normalnym?
P-value jest ściśle związany z rozkładem normalnym w kontekście testowania hipotez, szczególnie podczas przeprowadzania testów opartych na rozkładzie t lub rozkładzie normalnym.
W testowaniu hipotez badacze lub statystycy dążą do wyciągnięcia wniosków na temat populacji na podstawie próby. P-value reprezentuje prawdopodobieństwo uzyskania wyników tak ekstremalnych, jak obserwowane w próbie, przy założeniu, że hipoteza zerowa jest prawdziwa.
Hipoteza zerowa (H0) zazwyczaj reprezentuje domyślne założenie, takie jak „nie ma różnicy” lub „nie ma efektu”. Hipoteza alternatywna (Ha) reprezentuje twierdzenie lub efekt, który testujemy, często stwierdzając, że istnieje znacząca różnica lub skutek.
Rola wielkości próby w testowaniu hipotez
Kiedy wielkość próby jest wystarczająco duża (zwykle uważa się, że n > 30), a dane spełniają określone warunki, w grę wchodzi centralne twierdzenie graniczne. Stwierdza, że rozkład średnich z próby (lub innych statystyk) będzie miał tendencję do rozkładu normalnego, nawet jeśli oryginalne dane nie pochodziły z rozkładu normalnego.
W testowaniu hipotez statystykę oblicza się na podstawie danych z próby, a jej rozkład zależy od wielkości próby oraz leżącego u podstaw rozkładu populacji. Przy dużej próbie i rozkładzie normalnym populacji, dane użyte do próby statystycznej również mają rozkład normalny.
Jednak gdy odchylenie standardowe populacji jest nieznane, a wielkość próby jest mała (zwykle n <30), zamiast tego stosuje się rozkład t. Rozkład t jest podobny do rozkładu normalnego, ale zakłada mniejszą ilość próbek w pobliżu średniej wartości a większą przy „obszarach skrajnych” wykresu, co odpowiada za zwiększoną niepewność w małych próbkach.
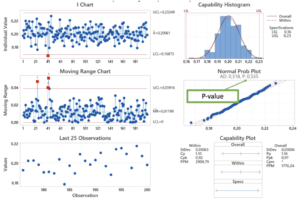
P-value jest następnie obliczana na podstawie statystyki testowej i powiązanego z nią rozkładu (normalnego lub t). W przypadku testu jednostronnego p-value reprezentuje obszar pod krzywą w „ogonie”. W przypadku testu dwustronnego reprezentuje prawdopodobieństwo zaobserwowania danych tak lub bardziej ekstremalnych w obu „ogonach”.
Jeśli jego wartość jest mała (zazwyczaj < 0,05), oznacza to, że zaobserwowane wyniki prawdopodobnie nie wystąpią przypadkowo, jeśli hipoteza zerowa jest prawdziwa. W takich przypadkach odrzuca się hipotezę zerową na rzecz hipotezy alternatywnej.
Podsumowując, P-value jest powiązany z rozkładem normalnym poprzez wykorzystanie rozkładu normalnego lub rozkładu t (dla małych prób) podczas przeprowadzania testów hipotez. P-value określa prawdopodobieństwo zaobserwowania danych, biorąc pod uwagę przyjęte założenia dotyczące rozkładu populacji i hipotezę zerową.
Podsumowanie
W dziedzinie statystycznej kontroli procesów rozkład normalny odgrywa kluczową rolę w zapewnianiu stabilności, przewidywalności procesów i możliwości spełnienia wymaganych specyfikacji. Jego symetria oraz zdefiniowane właściwości sprawiają, że stanowi nieocenione narzędzie do ustalania granic kontrolnych.
Dodatkowo, umożliwia analizę procesu i przyczyn źródłowych. Rozumiejąc i wykorzystując normalną dystrybucję, przemysł może usprawnić kontrolę jakości oraz zmniejszyć ilość odpadów. W efekcie dostarcza produkty i usługi, które przekraczają oczekiwania klientów.
Dariusz Kowalczyk


